初等变换
对矩阵的行初等变换可以分为以下三类:
-1)对调矩阵的两行,记为$ E_{i,j} = r_i \leftrightarrow r_j $
-2)将某一行的元素乘以非零常数,记为 $ E_{s} =r_i\times s $
-3)将某一行的元素乘以非零常数后,加到另一行上,记为$ E_{i,j(s)}r_i+r_j\times s$
定理1:
- 对一个矩阵$ A_{mn}$进行初等行变换相当于用相应的初等矩阵$ T_{mm}$左乘矩阵A。
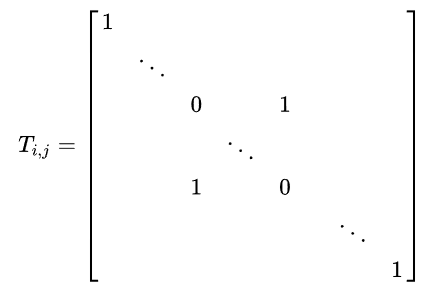
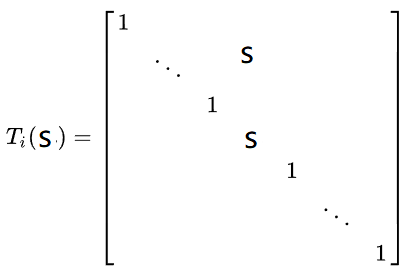
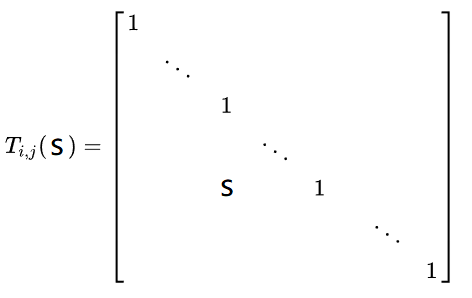
- 对一个矩阵$ A_{mn}$进行初等列变换相当于用相应的初等矩阵$T_{nn}$右乘矩阵A。
定理2: 任何初等矩阵E都是正交矩阵,即 \(E^TE = EE^T = I\)。
定理3: 任何正交矩阵的乘积仍然是正交矩阵。 $ A_1,A_2$是正交矩阵,即满足
\(A_1^TA_1 = A_1A_1^T = I\) \(A_2^TA_2 = A_2A_2^T = I\) 那么: \((A_1A_2)^TA_1A_2 = A_2^TA_1^T A_1A_2 = I\) \(A_1A_2(A_1A_2)^T = A_1A_2A_2^TA_1^T = I\)
即 $ A_1A_2$页是正交矩阵
根据定理1、定理2,可以得到:
定理4: 任何一个矩阵$ A_{mn}$可以初等变换变成一个对角矩阵。即:
\[A_{mn} = U_{mm} D_{mn} V_{nn}^T\]证明:对A进行一系列的初等行变换和初等列变换,可将A化为对角矩阵(如同高斯消去法)。即 \(E_hE_{h-1}\cdots E_{2} E_{1} A \hat{E_{1}} \hat{E_{2}} \cdots \hat{E_{k}} = D\)
\[A ={E_1}^T \cdots {E_h}^TD{\hat{E_k}}^T \cdots {\hat{E_1}}\]令 $U_{mm} = {E_1}^T \cdots {E_h}^T , {V_{mn}}^T = {\hat{E_k}}^T \cdots {\hat{E_1}} $。
即有:\(A_{mn} = U_{mm} D_{mn} {V_{nn}}^T\)
当然$U_{mm}, V_{nn}^T$都是正交矩阵,因为它们是初等矩阵的乘积。 因此:
\({U_{mm}}^TU_{mm} = U_{mm}{U_{mm}}^T = I\) \({V_{nn}}^TV_{nn} = V_{nn}{V_{nn}}^T = I\)
因为$ {A_{mn}}^T = V_{nn} {D_{mn}}^T {U_{mm}}^T $
因此:
\[A_{mn}{A_{mn}}^T U_{mm} = U_{mm} D_{mn} {V_{nn}}^T V_{nn} {D_{mn}}^T {U_{mm}}^T U_{mm} = U_{mm} D_{mn}{D_{mn}}^T\]令 $S_{mm} = D_{mn}{D_{mn}}^T $,这是一个对角矩阵,其中对角线上的值 $s_{ii} = d_{ii}^2$
同理,可以得到: \({A_{mn}}^T A_{mn} V_{nn} = V_{nn} {D_{mn}}^T {U_{mm}}^T U_{mm} D_{mn} {V_{nn}}^T V_{nn} = V_{nn}{D_{mn}}^T D_{mn}\)
令 $\hat{S_{nn}}={D_{mn}}^T D_{mn}$,这是一个对角矩阵,其中对角线上的值 $s_{ii} = d_{ii}^2$ ( i<=m)或0(i>0)
省略下标,即有:
\[AA^TU = U D_{mn}{D_{mn}}^T = US_{mm}\] \[A^TAV = V {D_{mn}}^T D_{mn} = = V \hat{S}_{nn}\]例如: \(D = \left(\begin{array}{ccc} d_{11}&0&0\\ 0&d_{22}&0\\ \end{array}\right)\)
\[D^T = \left(\begin{array}{cc} d_{11}&0\\ 0&d_{22}\\ 0&0 \end{array}\right)\]则:
\[D D^T = \begin{bmatrix} {d_{11}}^2 & 0 \\ 0 &{d_{22}}^2 \\ \end{bmatrix}\] \[D^T D = \begin{bmatrix} {d_{11}}^2 & 0& 0 \\ 0 &{d_{22}}^2& 0 \\ 0 &0 & 0 \end{bmatrix}\]定义:特征值和特征向量 对于一个矩阵B,如果由向量v,满足:$ Bv= \lambda v$,则称v是B的特征向量,而$\lambda$是对应的特征值。
因为 \(AA^TU = AA^T (U_1,N_2,\cdots, U_m) = (U_1 {d_{11}}^2,U_2{d_{22}}^2,\cdots, U_m{d_{mm}}^2 )\)
所以,矩阵$AA^T$的特征向量是U中的列向量,特征值就是$S_{mm}$中的对角线上相应的值。
同样,因为:
\[A^TAV = A^TA (V_1,V_2,\cdots, V_n) = (V_1 {d_{11}}^2,V_2{d_{22}}^2,\cdots, V_n{d_{nn}}^2 )\]所以,矩阵$A^TA$的特征向量是V中的列向量,特征值就是$\hat{S}_{nn}$ 中的对角线上相应的值。
同样的,可以得到下面的公式:
\[U = AVD^{-1}\] \[A^T = VD^TU^T\]参考:
Singular Value Decomposition (SVD) Tutorial: Applications, Examples, Exercises
您的打赏是对我最大的鼓励!
 支付宝打赏
支付宝打赏  微信打赏
微信打赏